Static Procedural Methods theorem (Barseghyan-2015) Reason1

Barseghyan (2015) deduces the Static Procedural Methods theorem as follows and with the following justification:1pp. 224-225

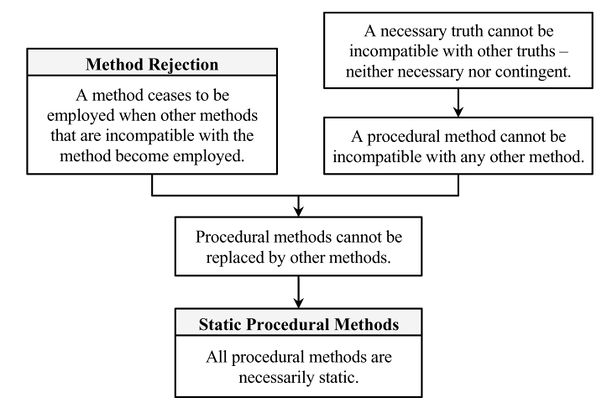
By the method rejection theorem, a method is rejected only when other methods that are incompatible with the method in question become employed. Thus, a replacement of a procedural method by another method would be possible if the two were incompatible with each other. However, it can be shown that a procedural method can never be incompatible with any other method, procedural or substantive.

Consider first the case of a procedural method being replaced by another procedural method. By definition, procedural methods don’t presuppose anything contingent: they can only presuppose necessary truths. But two necessary truths cannot be incompatible, since necessary truths (by definition) hold in all possible worlds. Therefore, two methods based exclusively on necessary truths cannot be incompatible either; i.e. any two procedural methods are always compatible. Consequently, by the method rejection theorem, one procedural method cannot replace another procedural method. Consider a new necessarily true mathematical proposition that has been proven to follow from other necessary true mathematical propositions. By the second law, this new theorem becomes accepted into the mosaic. The acceptance of this theorem can lead to the invention and employment of a new procedural method based on this new theorem. Yet, this new method can never be incompatible with other employed procedural methods, just as the newly proven theorem can never be incompatible with those theorems which were proven earlier (of course, insofar as all of these theorems are necessary truths).

Thus, the only question that remains to be answered here is whether a procedural method can be replaced by a substantive method? Again, the answer is “no”. Substantive methods presuppose some contingent propositions about the world, while procedural methods presuppose merely necessary truths. But a necessary truth is compatible with any other truth (contingent or necessary). Therefore, no newly accepted theory can be incompatible with an accepted necessary truth. In particular, if we take the principles of pure mathematics to be necessarily true, then it follows that no empirical theory (i.e. physical, chemical, biological, psychological, sociological etc.) can be incompatible with the principles of mathematics. Consequently, a new substantive method can never be incompatible with procedural methods. Take the above-discussed abstract deductive acceptance method based on the definition of deductive inference: if a proposition is deductively inferred from other accepted propositions, it is to be accepted. It is safe to say that no substantive method can be incompatible with this requirement, for to do so would mean to be incompatible with the definition of deductive inference, which is inconceivable. Thus, a procedural method can be replaced neither by substantive nor by procedural methods.

This brings us to the conclusion that all procedural methods are in principle static.

Here is the deduction:

This reason for Static Procedural Methods theorem (Barseghyan-2015) was formulated by Hakob Barseghyan in 2015.1